Bernoulli-Kette
Führt man ein Bernoulli-Experiment n mal durch, so spricht man von einer Bernoulli-Kette der Länge n.
Die Trefferwahrscheinlichkeit, also die Wahrscheinlichkeit für den "Ja"-Ausgang eines einzelnen Bernoulli-Experiments sei p.
Die Zufallsvariable X stehe nun für die Anzahl der Treffer.
Der Ausdruck
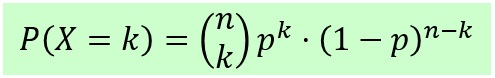
Binomialverteilung
Die Wahrscheinlichkeitsverteilung, die sich aus einer Bernoulli-Kette ergibt nennt man Binomialverteilung. Der Ausdruck P(X=k) (siehe oben) hängt tatsächlich nur von n und p ab. Man nennt die Zufallsvariable X daher Bn;p-verteilt.
Eigenschaften der Binomialverteilung
Zur besseren Veranschaulichung betrachten wir nun drei Bernoulli-Ketten der Länge 10.
Die Trefferwahrscheinlichkeit im ersten Experiment sei p=0,2 im zweiten p=0,5 und im dritten p=0,8.
Wir variieren also p und betrachten die zugehörigen Histogramme:
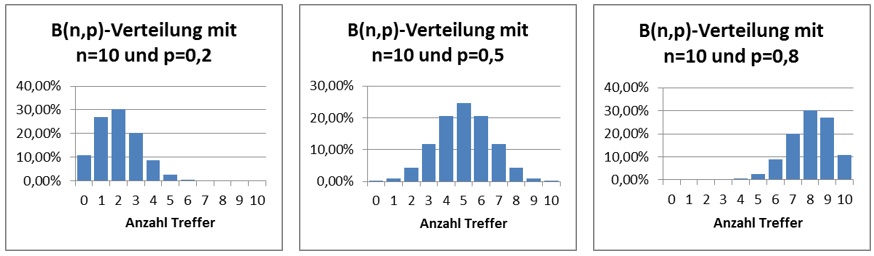
Dies sollte auch anschaulich klar sein, denn bei steigenden Trefferwahrscheinlichkeiten wird es auch immer wahrscheinlicher, mehr Treffer zu erzielen!
Variiert man die Anzahl n der Versuche, also die Länge der Bernoulli-Kette so verändert sich lediglich die Höhe der einzelnen Säulen im Histogramm, d.h. mit größer werdenden Versuchszahlen werden die einzelnen Trefferwahrscheinlichkeiten immer geringer.
Binomialverteilung mit dem GTR
Bei langen Bernoulli-Ketten ist man weniger an der Wahrscheinlichkeit einzelner Trefferanzahlen interessiert sondern eher daran, wie wahrscheinlich es ist, dass die Trefferanzahl sich in einem gewissen Bereich bewegt.
Eine Zufallsvariable X sei nun B10;0,4-verteilt.
Wie groß ist die Wahrscheinlichkeit für …
- mindestens 5 Treffer? ⇒ P(X≥5)=?
- höchstens 8 Treffer? ⇒ P(X≤8)=?
- weniger als 7 Treffer? ⇒ P(X<7)=?
- eine Trefferzahl zwischen 3 und 9? ⇒ P(3≤X≤9)=?
Lösung der Aufgaben
- Es gilt P(X≥5) = 1 - P(X≤4).
Eingabe mit dem GTR: 1 - binomcdf(10,0.4,4)
Dies liefert 0,3669, d.h. P(X≥5) ≈ 36,69%.
Man kann sich die Umwandlung des Ausdrucks P(X≥5) in die "kleiner-gleich-Schreibweise" anhand der folgenden Abbildung verdeutlichen: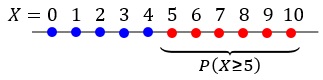
- P(X≤8) = binomcdf(10,0.4,8) ≈ 99,8%
- P(X<7) = P(X≤6) = binomcdf(10,0.4,6) ≈ 94,5%
- P(3≤X≤9) = P(X≤9) - P(X≤2) = binomcdf(10,0.4,9) - binomcdf(10,0.4,2) ≈ 83,2%
Die folgende Abbildung verdeutlicht den Zusammenhang: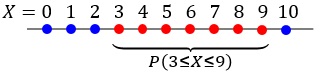
| Downloads |
PowerPoint